Set, as a recreational problem
During Chinese New Year visiting, my cousin introduced the game set to me.
The objective of the game is to identify a set of three cards from 12 cards laid out on the table. Each card has 4 features, each with three variants. The four features are Colour, Symbol, Number, Shading. A set consists of three cards in which each feature is either the same on each card or different on each card. Examples and rules here.
Set is surprisingly tricky as it is easy to miss out a feature and mis-identify a set. It is also a game that can be played alone, by competing against the clock, or in a group where multiple players compete to spot a set. Once spotted, the player can collect the cards as score. When a set is removed, three new cards are placed and the game resumes.
During the game, there were times where we couldn’t spot any sets, and we added three new cards to the table. This made me wonder whether it was always possible to find a set from any 12 cards. (I found this problem more interesting than the game 😛)
The answer is no, it is not always possible. An easy way to see it is to encode each card as a 4-tuple \((a,b,c,d)\) where \(a,b,c,d\) takes on the values from \({1,2,3}\). So a set of three cards looks something like \((1,2,2,1), (1,2,2,2), (1,2,2,3)\) which corresponds to one, two, three solid blue diamond (assuming the last component represents the count). Since each tuple is unique, a set must consist of a tuple with ‘3’ as one of the components. So to prevent a set, we could just count the possibilities without a 3. Suppose each component is only chosen from \({1,2}\), then since we’re choosing 4 components, there are \(2^4 = 16\) possibilities, which is \(> 12\). So we have constructed a counter example that there is always a set from any 12 cards. In fact this shows that there can still be no sets even when 3 additional cards are placed on the table.
A natural follow up is what is the maximum number of cards without a set. The naive way of choosing from \({1,2}\) gives a lower bound of 16, but can we do better? It turns out the answer is yes, there can still be no sets in 20 cards! But the proof is more involved than what I want this post to be. Interested readers can find an investigation here. Just know that in some rare cases, you can lay out 12 + 3 + 3 cards and still not have a set!
Another interesting extension to think about: What is the probability that there are no sets in a given 12, 15, 18 cards?
Yup that escalated quickly.
PS: Update 2023
I revisited this problem again in 2023 when I was introduced to another visual focused card game.
I reread my post and I was curious what was the maximal number of “Set-less” cards.
Rereading the linked investigation paper, I found the following the visual the easiest to proof without words.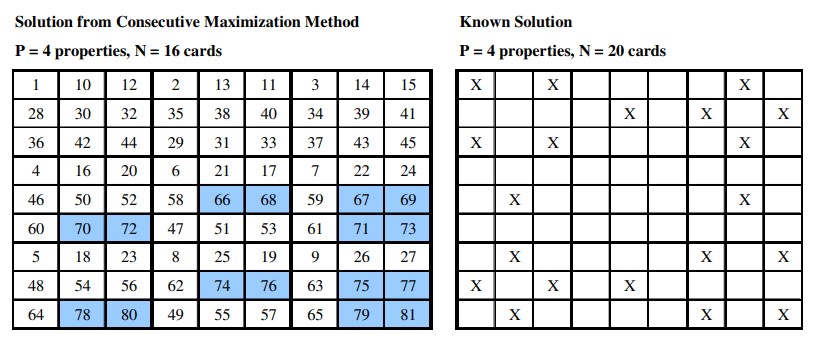
The paper was still an interesting read after all these years. This is the summary. The crux is the invariant - the total number of possible sets from the 81 cards over various partitions into 2 piles. Then one can come up with the
Observations: Each card is part of