Problem 26 in penguin book of puzzles.

A Walking Puzzle

A man set out at noon to walk from Appleminster to Boneyham, and a friend of his started at two p.m. on the same day to walk from Boneyham to Appleminster. They met on the road at five minutes past four o’clock and each man reached his destination at exactly the same time. Can you say at what time they both arrived?

What’s interesting and beautiful about this problem is the surprizing lack of information about speeds and distances; all you’re being told is the time.

Solution 1 - Forming equations.

Such algebraic problems ask for an element of faith that when you simplify the relevant equations, the unknowns cancel out and leave you with a simple equation.

The crux to this is to note that they met at 4:05pm and ended at some time T. This duration, call it $t$, is fixed so we can form an equation here. Let $ d_{xy} $ be the distance from point x to point y, and let m be the point which they met.

  • $ d_{mb}/s_a = t = d_{ma}/s_b $
  • $ s_a = d_{am}/(245\text{ min}) $
  • $ s_b = d_{bm}/(125\text{ min}) $
  • Substituting them into the first equation gives $ (d_{ma}/d_{mb})^2 = 245/125 $
  • Substituting $ s_a $ into the first equation, we get $t = (245\text{ min}) * d_{mb}/d_{ma} = 175 \text{ min} $

Solution 2 - Using distance time graph

My first attempt was to draw the time distance graph which looked a lot like the cross ladder problem mentioned in harmonic mean.

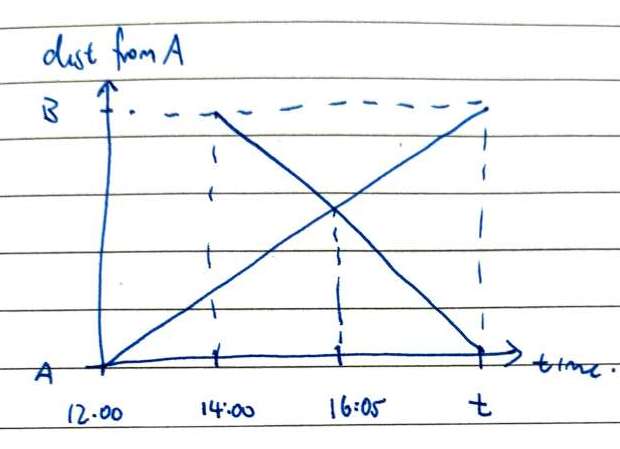
speed-time diagram
speed-time diagram
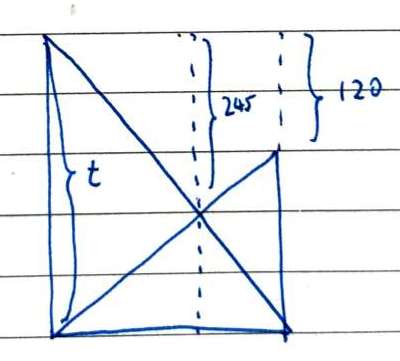
Crossed ladder diagram
Crossed ladder diagram

Putting it in the form, we get

$$ \frac{1}{t-245} = \frac{1}{t} + \frac{1}{t-120} $$

I felt clever doing it, but it turns out this equation is quite a pain to solve by hand because of the algebraic manipulation and then solving the quadratic.

We can first apply a translation $y = x - 60$ to make the RHS somewhat symmetric which reduces the amount of manipulation, but we still end up having to solve a quadratic.

Faithfully solving the equation, or if we’re lazy just key it into wolfram alpha, we get $ t = 420 $.

Thoughts

This question made me think about two things. First, equations involving reciprocals make the problem disproportionate tedious.

Second, what the general form of the solution to the equation looked like:

$$ \frac{1}{x-c} = \frac{1}{x-a} + \frac{1}{x+a} $$ $$ x^2 - a^2 = 2x (x-c) $$ $$ c^2 - a^2 = (x - c)^2 $$ $$ x = c \pm \sqrt{c^2 - a^2} $$