Problem 39 from the penguin book of puzzles.

A man named Jones set out to walk from A to B, and on the road he met his friend Kenward, ten miles from A, who had left B at exactly the same time. Jones executed his commission at B and, without delay, set out on his return journey, while Kenward as promptly returned from A to B . They met twelve miles from B. Of course, each walked at a uniform rate throughout. Now, how far is A from B?

Something similar yet different from the previous problem, this time you’re only told the distances.

Solution

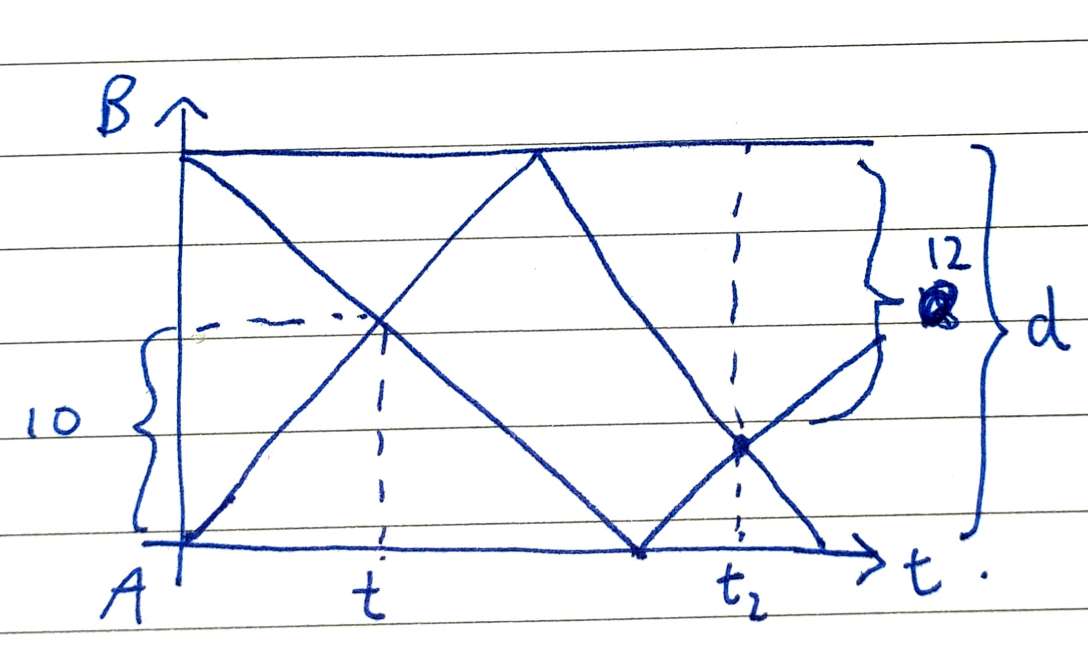
A distance-time graph would make it easier to visualize the the problem.

Let $d$ be the distance between A and B. The crux is to notice that When they met the second time, they have collectively covered $3d$. Similarly, the first time they met, they have collectively covered distance $d$. This means if they met at time t the first time, they will meet at time 3t the second time.

If we focus on Jones, and let his speed be $s$ and form equations based on the distance travelled, then $ 10/t = d + 18 / (3t) $. We then get $ d = 3 * 10 - 12 = 18 $

Thoughts

What’s interesting here is t doesn’t really matter. Indeed in our distance-time graph, we could have chosen any units we want. In order words, we could just normalize the time, or the speed. If we normalize time, such that $t = 1$, then $s = 10$, we’ll still have to make use of the fact that they meet the second time at $t = 3$, and Jones would have travelled 30 miles. From the diagram, we know that’s $d + 12 \rightarrow d = 18$.

Another interesting point is when they meet the second time, both will collectively travelled $3d$, so the distance between the two cities are always $3 * (\text{first distance}) - (\text{second distance})$!