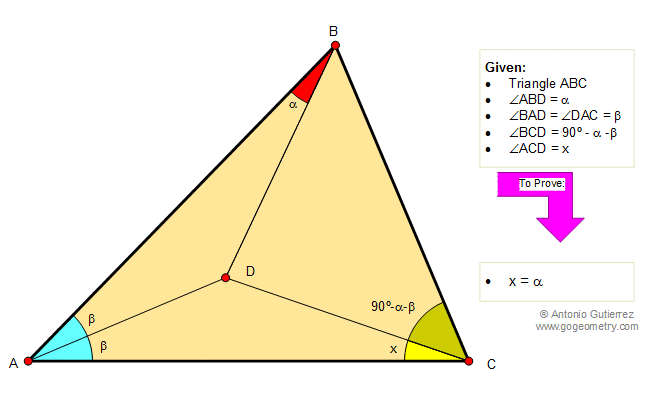
Found this while browsing and thought it was interesting. I’m still deciding whether this should live on this blog. Don’t permalink to this yet!
Technically there are two possible answers for x, but if you restrict ABC to be acute, then there is only one solution.
Posed differently:
- Given an angle A and an internal angle bisector of A
- Let $A = 2 \beta $
- Choose a point D on the bisector
- Choose B on one leg of the angle such that $DBA = \alpha$
- Find the loci of C on the other leg such that $DCB = 90^\circ -\alpha - \beta$
Solutions:
Stolen from the comments from the original source: Using Ceva’s theorem: We can simplify it to become $$ \frac{\sin(\alpha)}{\sin(\pi/2-\beta-x)} \cdot \frac{\sin(\pi/2 - \alpha - \beta)}{\sin(\beta)} = 1 $$
Using trigo product to sum formula, we get
$$ sin(2\alpha + \beta) = sin(2x + \beta) $$
Which reduces to $ x = \pi/2-\alpha - \beta $ or $ x = \alpha$
A section solution
Without using Ceva’s theorem, someone posted an alternate solution:
- If AC = AB, then AD is also the altitude and things becomes obvious.
- Suppose AC is not equal to AB, then find E on AC extended so that AE = AB.
- Then DBEC is concyclic, and by the same argument, $DEC = \alpha$
- DBC = DEC = $\alpha$.
- D is the incenter. $x = \pi/2 - \alpha - \beta$