These are some notes on harmonic mean taken some time in 2016.

Harmonic mean

We start by introducing three number sequences:

  • An Arithmetic Progression (AP) is given by $a$, $a + d$, $a + 2d$, …
  • A Geometric Progression (GP) is given by $a$, $ar$, $ar^2$, …
  • A Harmonic Progression (HP) is given by $\{1/a_i\}$ where $\{a_i\}$ is an AP.

Given a number sequence, we can define its mean. We use two here for simplicity.

  • An arithmetic mean (AM) is given by $(a + b)/2$
  • A geometric mean (GM) is given by $\sqrt{ab}$ or $(ab)^{(1/2)}$
  • A harmonic mean (HM) is given by $\frac{2}{(1/a + 1/b)}$

Geometric interpretations

On it’s own, the above can be rather dry. However, there are some interesting geometric interpretations.

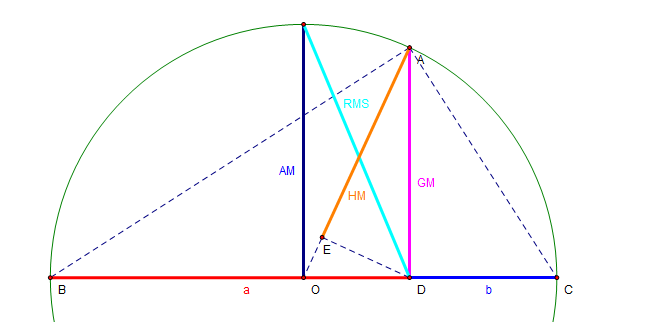
Visual comparison against other means

Given a semi circle, we can plot the length of all the means as follows. What’s interesting is all the inequality drops out naturally.

Proof:

  • AM: Half the diameter (a+b).
  • GM: $ ADB \sim CDA \rightarrow AD/DB = CD/DA \rightarrow AD = \sqrt{CD*DB} $
  • HM: $ AED \sim ADO \rightarrow AE/AD = AD/AO \rightarrow AE = \frac{ab}{(a+b)/2} $

Height of inscribed triangle

In the following diagram, x is half the harmonic mean of a and b. Another way to see it is the reciprocal of x is the sum of reciprocal of a and b.

Proof (sketch):

  • By similar triangles $ x/a = u / (u+v) $ and $ x/b = v /(u+v) $
  • Add them together to get $ x(1/a + 1/b) = 1 $

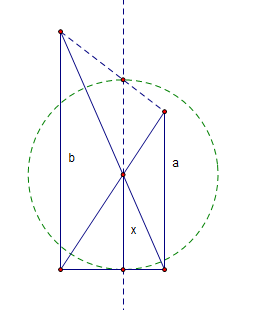
Intersection of altitudes

Similarly, the same is true in the following.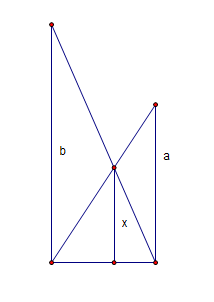

Proof (sketch): Let the two segments on the base be u, v. Repeat the argument above.

Intersection of trapezium’s diagonals

If we draw the dotted line to turn it into a trapezium, then the line parallel to the two sides passing through the diagonals is the harmonic mean of the two parallel lengths.

Interesting inequalities and relations

  • $ HM \le GM \le AM $
  • HM, GM, AM forms a GP, ie $ HM * GM = AM ^2 $
  • $a$ and $b$ are the roots of the quadratic $x^2 - 2Ax + G^2 = 0$
  • $a$, $b$ and $c$ are the roots of the cubic $x^3 - 3Ax^2 + (3G^3/H) - G^3 = 0$ where A, G, H are the respective means of the roots.
  • Given AM, GM, we can recover a, b: $A \pm \sqrt{(A-G)(A+G)}$

Applications in real life

HM is in some sense the “true average of rates”. This is illustrated by a simple puzzle:

Suppose a car travels from A to B at 60km/h and then from B to A at 40km/h, what is its average speed?

The average is given by the HM, which is 48km/h in this case.

We can see this in various applications such as finding the density (which is the rate of mass) of alloy given the density of the constituents. In physics, calculating the effective resistance of electrical resistors in parallel is related to the harmonic mean as well.

In information retrieval, the harmonic mean of precision and recall, called the F-measure is used to measure the performance of algorithms and systems.

Conclusion

I will leave you with a simple puzzle.

A bathtub has two taps. Each tap can fill the tub to the brim in 1 hour and 2 hours respectively when it is the only tap running. How long will it take to fill the tap to the brim if both of them are opened at the same time?

Further reading