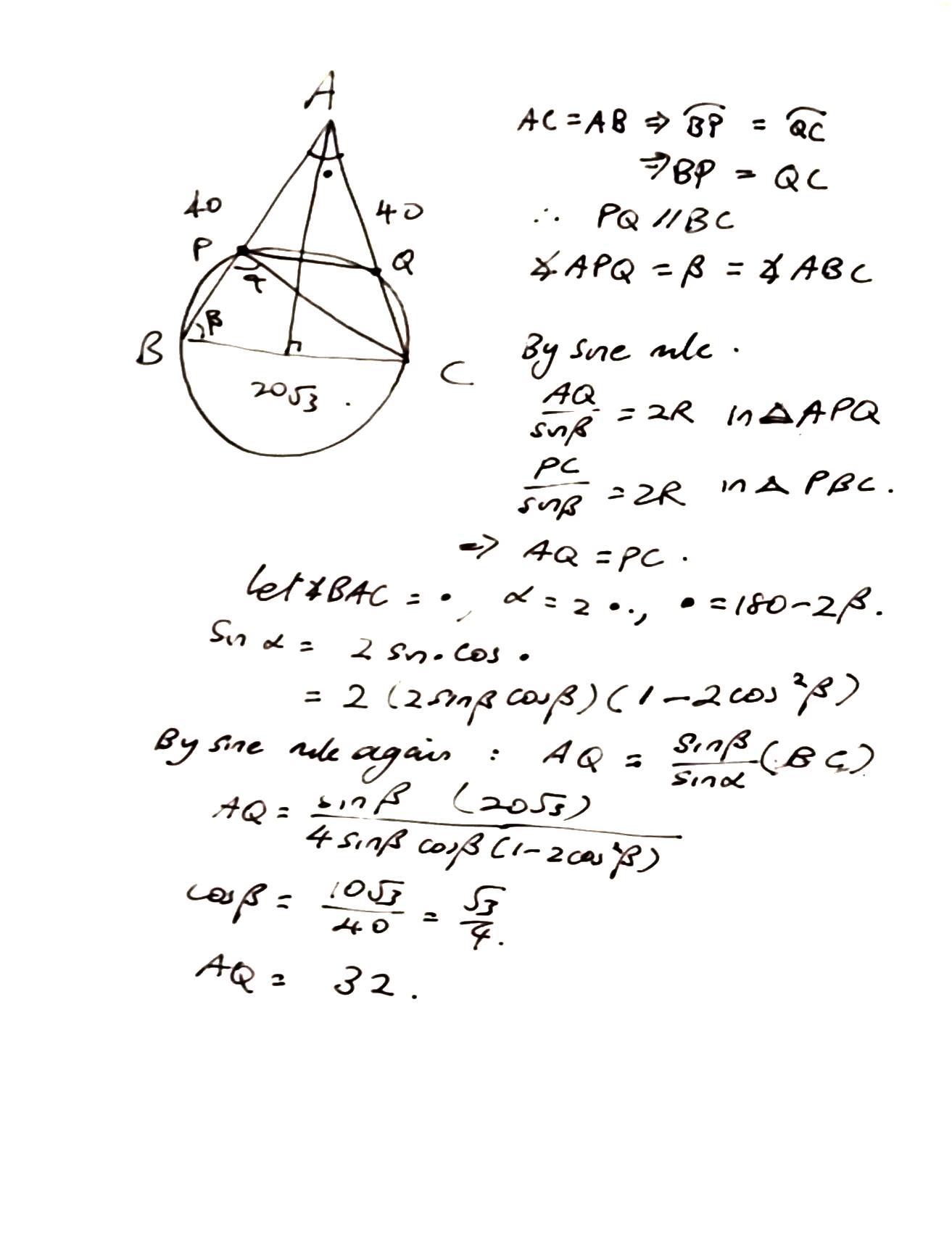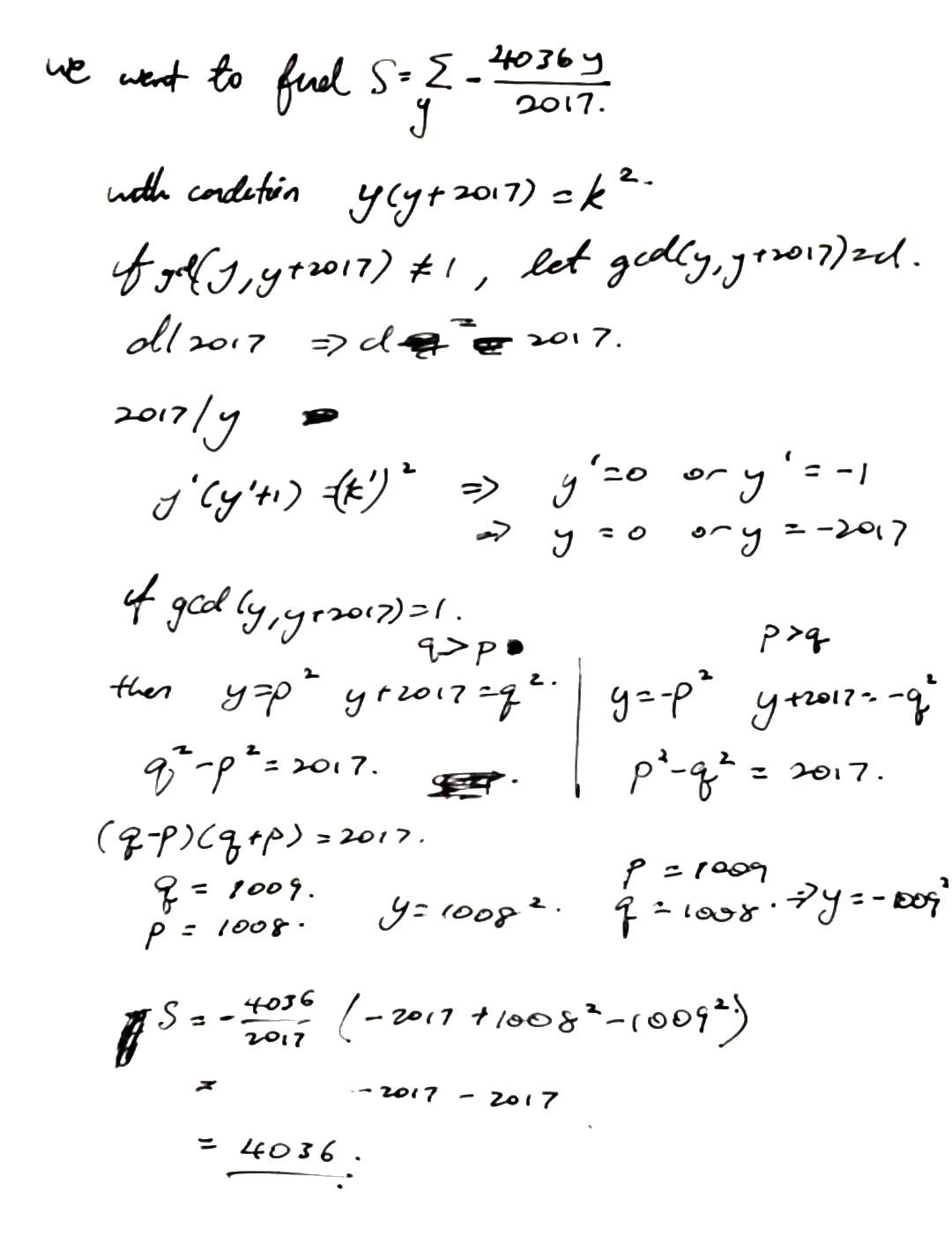The IMO 2017 took place recently, and I am feeling nostalgic.

I wanted to find out if I still had what it takes to do maths. So I got hold of the Singapore Maths Olympiad paper and had a go. This post is about the hours I spent doing the questions and my solutions. They are my own work so they may have mistakes.

If you are keen, do attempt the questions first before reading my solutions. If you’re short of time, I recommend just looking at Q7, Q20, Q22, Q25. Those are my favourite in this paper.

Also, for the really keen readers out there. If you have a nicer solution, feel free to share them with me.

Problems

Proofs have been abbreviated.

Solutions

1

Seems like a good warm up question. For S to be an integer, $ \sqrt{4-x^2} $ and $ \sqrt{4-x^2} $ must be non-negative, otherwise you can’t get rid of imaginary parts. $ x^2 >= 4 $ and $ x^2 <= 4 $ means that $ x^2 = 4 $. So $ x = \pm 2 $. $ x $ cannot be 2 because the first term will be undefined. Hence $ S \equiv 3^{2017} \equiv 3 \pmod{10} $.

2

This is such an overused question. This was a question when I was doing it > 10 years ago. Nonetheless, good warmup.

This is made easy by a trick where if you group the terms properly, squaring them usually results in a perfect square so you can undo the squaring.

$$f(a,b) = \sqrt{a + \sqrt{b}} + \sqrt{a - \sqrt{b}}$$ $$f(a,b)^2 = 2a + 2(a^2 - b)$$

In this case we want to find $$f(17, 288) - f(7, 49) = \sqrt{36} + \sqrt{16} = 20$$

3

This is also another pretty standard question. Each term simplifies to (2/(n)(n+1)) which can be written as 2(1/n - 1/n+1). That series telescopes and T becomes 2(1/1 - 1/2017). So 2017*T = 4032

4

Integration is also the area under the graph. So by drawing the graph $$y = \lfloor{x}\rfloor$$ We see that we are summing piecewise blocks of width 1. 55 is also easily recognisable as $$ \sum_1^{10} i$$ So a = 11

5

Let’s call the third line n. Since n is the angle bisector, the angle between l and n, and n and m are the same, so the magnitude of the dot product of the angle are the same too. Forming an equation with that, we get $$ (1, 2, -2) \cdot (c, 1, 0) = (c, 1, 0) \cdot (2, -1, 2) \Rightarrow c = 3$$

Next, we know the two lines intersects (implied by the angle bisector), so equating l and m, we get an equation in λ and µ. Equating m and n, we get another equation in μ and ω. Normally this would be unsolvable since there are 3 unknowns but only 2 equations. However, since they intersect, they are really in 2D space. So with some algebraic manipulation, we can solve for λ,μ,ω and get a = 7, b = -3. After enough grit, | a + b + c | = 7

6

Just work through the expansion. Ans: 7.

7

The warmup is over. This took me a while, because I led myself into a wild goose chase. Let me start with the nice solution, and then talk about the wild goose.

First, let’s try and get our hands dirty and enumerate all ways to write the sum for small numbers.

For 4:
1111
112
22
4

For 5:
11111
1112
122
23
5

For 6:
111111
11112
1122
222
33
6

It appears that the length each new possibility (after sorting) only shrinks by one. We should try and prove this. Suppose we have a long line (n times of each number is more than sufficient) of integers 1 1 … 1 2 2 … 2 3 … 3 …, and we start with a window of length k. We ask the question how many ways are there to place this window of length k such that the sum is equal to n. Clearly the only way for length n is to place the window at the start so we capture n 1’s. Now, what about k-1? We note that as we move the window rightward along this line, the sum either stays the same or increases by one. So as we move right, we eventually find the place to put our window of size k-1. We can see that this is unique because moving it rightwards would only increase the sum. Since we found ourselves a bijection, the answer for the case n = 2017 is 2016.

PS: The wild goose chase I started with was trying to calculate the number of solutions for each category (1->2, 2->3, etc) which can be thought of as counting the number of solution to the diophantine equation: $$a(k) + b(k+1) = 2017$$

Although it can be systematically solved, it requires way too many computations for it to be solvable during the competition.

8

The numbers in this question scream of rotations because of the 60 degrees, and Pythagoras because it is very close to the 6-8-10 triangle. Since we have a 30 deg angle, let’s try to make it 90 deg. Rotating ABC about point B counter clockwise 60 deg to A’BD makes the solution obvious. A’B = AB = 6 and angle A’AD = 90, so AC = A’D = 10.

9

Since ABC is isosceles, angle ABC is 30 deg. Drop the perpendicular from A to BC, call it Q. Then AQ = 1/2 * BC * tan 30 deg. And we also know DQ = 1/2 BC - BD = 5. So by pythagoras, we can find the length of AD. Ans: 10

10

After making two important observations: PQ // BC and AP = PC, the rest is just an application of trigonometric formula and the answer just drops out.

11

This seems like a “don’t overthink it question”. My first instinct was to apply some fancy inequality try to force equality to happen. However, if we simply replace a by 8 - (b + c + d), and similarly for the other terms, and let the value of what we want to find be T, then

$$ \frac{T}{10} + 4 = \frac{3}{10} \Rightarrow T = 36 $$

12

This seems to be like a standard complex number question, so let’s see where that brings us. Rewrite the definition as

$$ z_n = \sqrt{3}^n e^{i \frac{5}{6}\pi n} $$ Then the condition we want to satisfy becomes $$ |z_n (z_1 - 1)|^2 > 7000 \Rightarrow |z^n|^2 |z_1-1|^2 > 7000$$ By drawing the vector z_1-1 and then working out the length of the new vector, $$ |z_1 -1 | ^2 = 7 $$ The problem becomes finding minimum n such that $$ |sqrt(3)^n | > 1000 $$ Which is an easy enough problem, giving the answer 13.

13

The condition we have looks a lot like the cosine rule, so let’s try that and see what happens. By cosine rule, $$ a^2 = b^2 + c^2 - bc \sqrt{3} $$ Combining with the given equation, we have $$ c = b (\sqrt{3} -1)$$

If we split AC into AD and DC where D is the foot of the perpendicular from B to AC, then AD = cos(30deg) * c, and we can find tan C = -(sqrt(3) + 2).

It was a long shot, but I decided to find tan 2C, which simplifies to sqrt(3), which is tan 30 deg, so C = 15 deg.

14

Intuition suggests that the number will cease to be a square fairly quickly so we should be able to brute force it. To prove it, we should consider mods. Using either mod 7 or 5 will give us the solution, since we can stop after summing to 7! or 5! Ans: n=3

15

323 = 17 * 19. If p,q are coprime, then pq | f(x) iff p | f(x) and q | f(x). This suggests we should take the modulus of the expression. Using mod 17, we get n has to be even. Using mod 19, we also get that n has to be even. So we simply count the number of even n in the range. Ans: 1008

16

If we let the number of apples, oranges and pears in the first box be a, b, c respectively. Then the condition can be written as $$ (674 - a) (674 - b) (674 -c) = abc$$

To make our manipulation easier, let 674 = 2x, then after expanding and factorizing,

$$ (x-a)(x-b)(x-c) = x^2(a+b+c-3x) $$ But we know x = 337, which is prime and 0 < a,b,c < 674 So the only way we get x^2 on the RHS is if two of a,b,c are 337. But that forces the third to be 337 as well. So there is only 1 way.

17

Integer solution suggests we should consider the discriminant. Discriminant in X has to be a square, which simplifies to $$ (y)(y + 2017) = k^2 $$

Now, either y and y + 2017 are coprime or they are not. If they are, then both y and y+2017 are squares. Then either (y = p^2, q^2 - p^2 = 2017) or (y = -p^2, p^2 - q^2 = 2017), and we can solve this to get the solutions (y = -1009^2, y = 1008^2)

If y and y+2017 are not coprime, then let d be the gcd, then gcd | 2017 => gcd = 2017. Reduce the equation to get z(z+1) = w^2, which implies z = 0 or z = -1

Now, to get the sum of all the roots of x for a quadratic polynomial Ax^2 + Bx + C, we only need to find -B/A, which is known. So the answer we want is

$$ \sum_{y = 0,-1,-1009^2,1008^2} -\frac{4036y}{2017} = 4036 $$

18

EDIT: Another problem solver pointed out an elegant solution to this. After completing the quadratic, one can interpret f(x) as the sum of distance from point (-10, 15) and (5, 17) to a point (0,x). If we invert the latter in the x-axis to (5, -17), then it is apparent the minimum f(x) is the shortest distance between the two points, which is the length of the line joining (-10, 15) to (5, -17).

At first look, it seems like we can consider the two terms separately. Square root of a quadratic equation intuitively is going to look like a U shape around the stationary point. So let’s try and complete the square to see what we get:

$$ f(x) = \sqrt{(x-5)^2 + 17^2} + \sqrt{(x+10)^2 + 15^2} $$ Which looks primising. The minimum of the sum will be at the intersection, since the growth of each function will be bigger than the decrease in y value from the other due to the concavity.

Equating the two components give x = -11/30. So now the task is to estimate the floor of f(x).

$$ \sqrt{5.37^2 + 289} + \sqrt{9.63^2 + 225} = \sqrt{317.8} + \sqrt{317.7} $$

By some trial and error, we can estimate sqrt(317) ~ 17.8. Hence, the answer we want is 35.

19

Since we only care about the units digit, we only need to consider sums of the units digit, which cycles with a period of 10. In particular, the sum of every group of 20 consecutive numbers is 0 mod 10. If S(n) is the sum of the unit digits from of the sum 1 to n, then S(n) === S(n mod 20) mod 10. 2017^2017 mod 20 === -3 ^2017 mod 20. The order of -3 mod 20 is 4 (by enumerating), so -3 ^2017 === -3 === 17 mod 20. $$ S(2017^{2017}) \equiv S(17) \equiv 17*9 \equiv 3 mod 10 $$

20

I was stuck at this question for a very long time.

Rearrange to get

$$ a_{n+1} = a_n + \frac{1}{a_n} $$

I had many approaches, all of which failed. At first, I thought perhaps a graphical representation might lead somewhere. This sort of iteration relation can be visualized by drawing the graph of y = x + 1/x and x, and then drawing a zig-zag line starting from x = a_0. But this series doesn’t converge, so this approach doesn’t really help.

Next, what if we express a_n as p_n/q_n? We can get a recurrence relation for p_n and q_n, but the formula for calculating a_1000 is extremely unwieldy. So it seems hardly useful here.

What if we transform it into some sequence, using cosh and ln:

$$ a_{n+1} = 2 cosh(ln(a_n)) $$

Not even sure if there is a closed form for this.

So the next thing to try is to estimate this and bound it between two known values. x + 1/x is asking to be squared. So let’s try that

$$ a_{n+1} ^2 = 2 + a_n^2 + \frac{1}{a_n^2} $$ $$ a_n^2 = 2*n + a_0^2 + \sum_{i=0}^{n-1} \frac{1}{a_i}^2 $$

Since we only want a bound, we can pray and hope that the sum on the RHS can be bounded by some constant.

$$ \sum_{i=0}^{n-1} \frac{1}{a_i}^2 > n * 1/a_0 ^2 $$

This looks very promising! Substituting n = 1000, and a0 = 5, we have

$$ 2025 < a_n^2 < 2025 + \frac{2000}{25} $$

$$ \lfloor a_n \rfloor = 45 $$

21

At first, I thought I had to use the divisibility test for 7, which is in my opinion ugly, so there should be nicer way. Let’s see how many possibilities are there if we only use the divisibility test for 3.

It turns out that reduces the possibilities by quite a number!

Possible digit sets whose numbers are divisible by 3
3333333 -> 1 possibility
3333777 -> 7C3 = 35 possibilities
3777777 -> 7C1 = 7 possibitilies

At this point, I was wondering if doing 43 divisions is a sensible expectation for the competition. I decided yea. I didn’t actually bother doing it though.

22

Update: A problem solver pointed out my solution was not optimal with a counter example. So this is the new proposal: Start with a 1-colour grid. Colour the diagonals with different colours. Then colour the off diagonals on both sides with different colours, taking care of wrap around cases. With this method, one can get 6 * 20 + 1 = 121 colours.

Proof is still needed though.

Trying with small cases, it seems like one possible heuristic is a greedy algorithm, where you set the a n*n subsquare to have all different colours, and have the rest of the row and column protruding from it be of the same colour:

AB
CD

For the case where n = 
abc zzzzzz
def zzzzzz
ghi zzzzzz
zzz ...
zzz
zzz

If A is a n * n square, A will have n*n different colours, C and B will be filled with one colour each, and then we can reduce the problem to a sub problem with sub greed D.

Using this heuristic, the solution will be 6^2 + 6^2 + 6^2 + 4 + 1.

The interesting part is how to prove that that is the best solution, and what n should be. I couldn’t get a satisfactory proof. Parking this question for now. If you have a good suggestion, let me know!

23

The question is just asking to be looked at in base 2 and 3. We notice whether a set is chosen is based on the base 2 representation of of n, so if n is 5 = 101 in biary, then we choose the third, and the first element in the subset (ie converting that representation into base 3. 217 = 11011001 in binary, so the value we want is 11011001 in base 3 = 3^7 + 3^6 + 3^4 + 3^3 + 3^0 = 2187+729+81+27+1

24

This question really confuses me, because if we rationalize the root, and calculate a_11, we get -2sqrt(3), and a_12 = 2sqrt(3) again. So it seems like this will go on and a_2017 = a_11 = -2sqrt(3). The answer: 12.

25

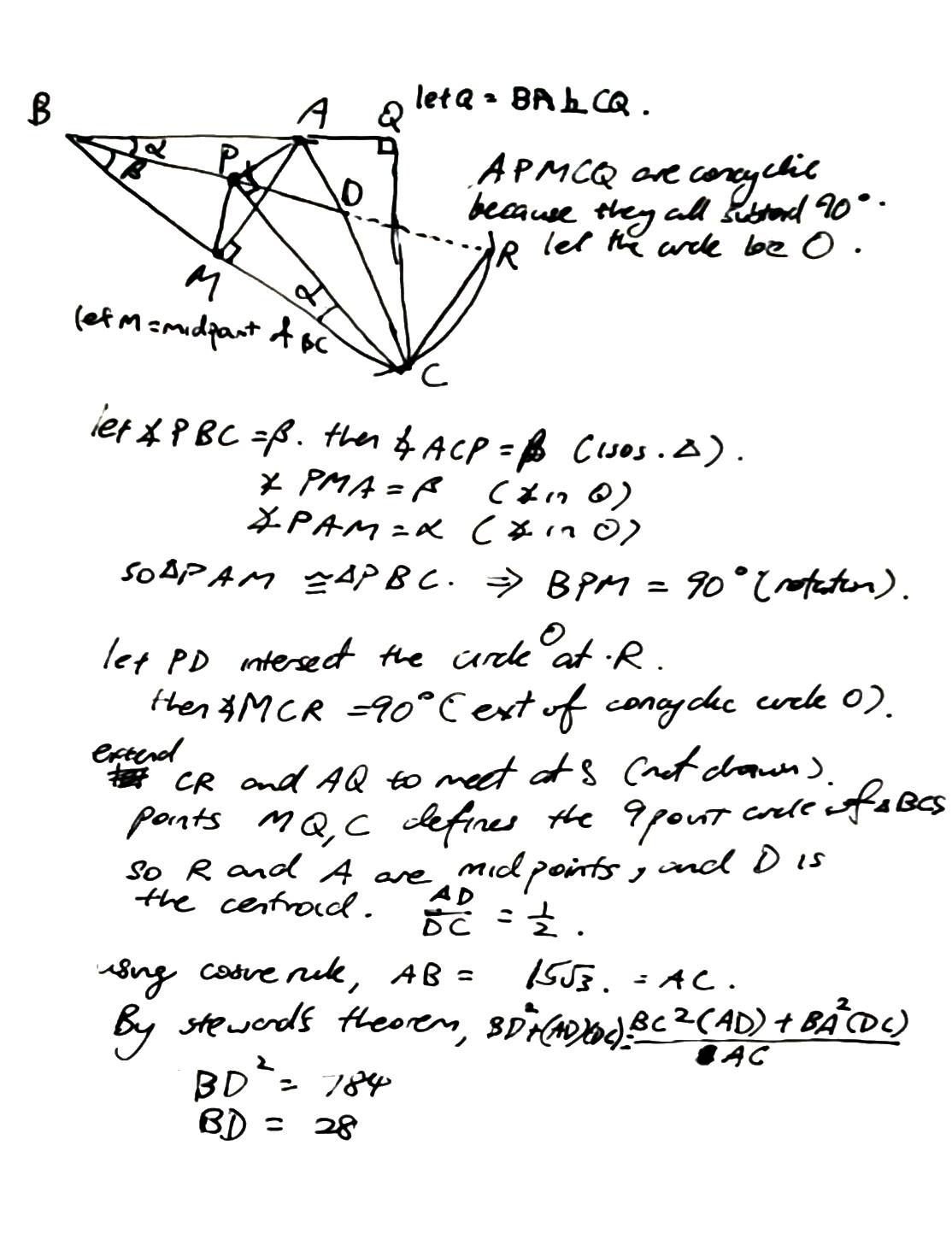
This is one killer question for me. Either I am missing something and overkilling it, or it really expects people to have a very strong geometric knowledge.